electric flux through box

2024-11-23T03:40:14 | By 2008 mustang metal thermostat housing , DOD blog

electric flux through box According to Gauss’s law, the flux of the electric field $\vec{E}$ through any closed surface, also called a Gaussian surface, is equal to the net charge enclosed $(q_{enc})$ divided by the permittivity of free space $(\epsilon_0)$: $250.00

0 · why does electric flux exist
1 · how to determine electric flux
2 · flux of electricity
3 · flux of electrical field pdf
4 · flux of an electric field
5 · electric flux through cubes
6 · electric flux physics
7 · electric flux definition pdf

$299.99

why does electric flux exist

1. Charge and Electric Flux - A charge distribution produces an electric field (E), and E exerts a force on a test charge (q 0). By moving q 0 around a closed box that contains the charge .

metal fabrication chesterfield

The electric flux through the top face (FGHK) is positive, because the electric field and the normal are in the same direction. The electric flux through the other faces is zero, since the electric field is perpendicular to the normal vectors of those .According to Gauss’s law, the flux of the electric field $\vec{E}$ through any closed surface, also called a Gaussian surface, is equal to the net charge enclosed $(q_{enc})$ divided by the permittivity of free space $(\epsilon_0)$:Therefore, we find for the flux of electric field through the box \[\Phi = \int_S \vec{E}_p \cdot \hat{n} dA = E_pA + E_pA + 0 + 0 + 0 + 0 = 2E_p A\] where the zeros are for the flux through the other sides of the box.Naturally, the more charge in a region bounded by a box, the more electric field lines one would expect to pass through the box. Thus, one would expect some relationship between the regional charge distribution and the electric field.

As in Figure 3b, the inward electric flux on one side exactly compensates for the outward electric flux on the other side. Therefore, in all of the cases shown in Figure 3, no net charge is enclosed in the box and there is no . Consider a closed triangular box resting within a horizontal electric field of magnitude E = 7.80 & 104 N/C as shown in Figure P24.4. Calculate the electric flux through (a) the vertical rectangular surface, (b) the slanted .

electric flux through the cube is the sum of fluxes through the six faces. Here, the net flux through the cube is equal to zero. The magnitude of the flux through rectangleBCKFis equal to the .In this video, we will learn about electric flux and how it is related to the work equation for a constant force. We will also use the equation for electric flux to determine the net electric flux .

The quantity $EA_1$ is the electric flux through $S_1$. We represent the electric flux through an open surface like $S_1$ by the symbol $\Phi$. Electric flux is a scalar quantity and has an SI unit of newton-meters squared per coulomb ($N \cdot m^2/C$).1. Charge and Electric Flux - A charge distribution produces an electric field (E), and E exerts a force on a test charge (q 0). By moving q 0 around a closed box that contains the charge distribution and measuring F one can make a 3D map of E = F/q 0 outside the box. From that map, we can obtain the value of q inside box.The electric flux through the top face (FGHK) is positive, because the electric field and the normal are in the same direction. The electric flux through the other faces is zero, since the electric field is perpendicular to the normal vectors of those faces.According to Gauss’s law, the flux of the electric field $\vec{E}$ through any closed surface, also called a Gaussian surface, is equal to the net charge enclosed $(q_{enc})$ divided by the permittivity of free space $(\epsilon_0)$:

Therefore, we find for the flux of electric field through the box \[\Phi = \int_S \vec{E}_p \cdot \hat{n} dA = E_pA + E_pA + 0 + 0 + 0 + 0 = 2E_p A\] where the zeros are for the flux through the other sides of the box.Naturally, the more charge in a region bounded by a box, the more electric field lines one would expect to pass through the box. Thus, one would expect some relationship between the regional charge distribution and the electric field.

electric flux through the cube is the sum of fluxes through the six faces. Here, the net flux through the cube is equal to zero. The magnitude of the flux through rectangleBCKFis equal to the magnitudes of the flux through both the top and bottom faces.In this video, we will learn about electric flux and how it is related to the work equation for a constant force. We will also use the equation for electric flux to determine the net electric flux through the closed surface of a right triangular box with uniform, horizontal electric field.The quantity $EA_1$ is the electric flux through $S_1$. We represent the electric flux through an open surface like $S_1$ by the symbol $\Phi$. Electric flux is a scalar quantity and has an SI unit of newton-meters squared per coulomb ($N \cdot m^2/C$).1. Charge and Electric Flux - A charge distribution produces an electric field (E), and E exerts a force on a test charge (q 0). By moving q 0 around a closed box that contains the charge distribution and measuring F one can make a 3D map of E = F/q 0 outside the box. From that map, we can obtain the value of q inside box.

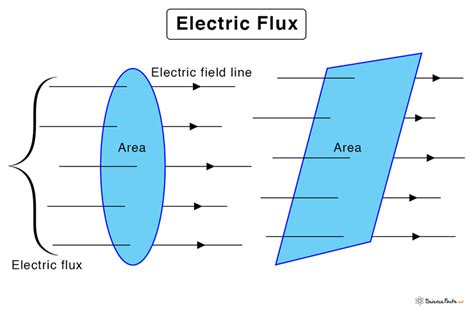
why does electric flux exist

The electric flux through the top face (FGHK) is positive, because the electric field and the normal are in the same direction. The electric flux through the other faces is zero, since the electric field is perpendicular to the normal vectors of those faces.According to Gauss’s law, the flux of the electric field $\vec{E}$ through any closed surface, also called a Gaussian surface, is equal to the net charge enclosed $(q_{enc})$ divided by the permittivity of free space $(\epsilon_0)$:Therefore, we find for the flux of electric field through the box \[\Phi = \int_S \vec{E}_p \cdot \hat{n} dA = E_pA + E_pA + 0 + 0 + 0 + 0 = 2E_p A\] where the zeros are for the flux through the other sides of the box.

Naturally, the more charge in a region bounded by a box, the more electric field lines one would expect to pass through the box. Thus, one would expect some relationship between the regional charge distribution and the electric field. As in Figure 3b, the inward electric flux on one side exactly compensates for the outward electric flux on the other side. Therefore, in all of the cases shown in Figure 3, no net charge is enclosed in the box and there is no net electric flux through the surface of the box.

Consider a closed triangular box resting within a horizontal electric field of magnitude E = 7.80 & 104 N/C as shown in Figure P24.4. Calculate the electric flux through (a) the vertical rectangular surface, (b) the slanted surface, and (c) the entire surface of the box.electric flux through the cube is the sum of fluxes through the six faces. Here, the net flux through the cube is equal to zero. The magnitude of the flux through rectangleBCKFis equal to the magnitudes of the flux through both the top and bottom faces.

how to determine electric flux