a no charge box surrounds a conducting metal sphere Non-Uniformly Charged Sphere. A non-conducting sphere of radius R has a non-uniform charge density that varies with the distance from its center as given by \[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\] where a is a constant. We . See current scrap price for Tin as of November 15, 2024. Check 30-day price chart for Tin and learn when to hold or sell your scrap metal. Price available for United States & Canada.
0 · non conducting solid sphere laws
1 · non conducting solid sphere
2 · conductive sphere no charge
3 · conducting sphere with no charges
4 · charge enclosed by sphere zero
5 · charge enclosed by sphere
6 · charge enclosed by conductive sphere
7 · 0 charge in conductor
This guide answers this question and provides useful tips and strategies for successfully integrating mixed metals into home decor. Can You Mix Metals in Your Home? Intentionally mixing metals within a space is a trend .
The reasoning provided behind why the electric field inside a metallic conductive sphere is zero, in my textbook is - "In case of a metallic (conducting) sphere, the entire charge will reside on the outer surface of the .
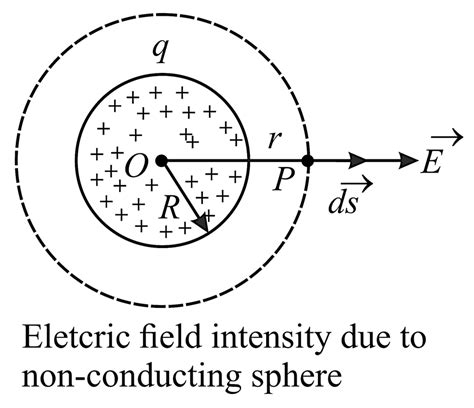
Consider a positive point charge Q located at the center of a sphere of radius r, as shown in Figure 4.2.1. The electric field due to the charge Q is 2 0 E=(/Q4πεr)rˆ ur, which points in the .We now study what happens when free charges are placed on a conductor. Generally, in the presence of a (generally external) electric field, the free charge in a conductor redistributes and very quickly reaches electrostatic equilibrium.Non-Uniformly Charged Sphere. A non-conducting sphere of radius R has a non-uniform charge density that varies with the distance from its center as given by \[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\] where a is a constant. We .• Surface S3 encloses no charges. Net flux through the surface is zero. The flux is negative at the upper part, and positive at the lower part, but these cancel. F = 0. • Surface S4 encloses both .
Apply the Gauss’s law strategy given above, where we work out the enclosed charge integrals separately for cases inside and outside the sphere. Solution Since the given charge density function has only a radial dependence and no .Child acquires electric charge by touching a charged metal sphere. Electrons coat each individual hair fiber and then repel each other. A charge distribution produces an electric field (E), and E .

non conducting solid sphere laws
Charging by conduction involves the contact of a charged object to a neutral object. Suppose that a positively charged aluminum plate is touched to a neutral metal sphere. The neutral metal sphere becomes charged as the result of . A uniform electric field has zero net flux through a closed surface containing no electric charge. Example: Electric flux through a sphere. A point charge is surrounded by an . The reasoning provided behind why the electric field inside a metallic conductive sphere is zero, in my textbook is - "In case of a metallic (conducting) sphere, the entire charge will reside on the outer surface of the sphere. Therefore .
The lowest potential energy for a charge configuration inside a conductor is always the one where the charge is uniformly distributed over its surface. This is why we can assume that there are no charges inside a conducting sphere.Consider a positive point charge Q located at the center of a sphere of radius r, as shown in Figure 4.2.1. The electric field due to the charge Q is 2 0 E=(/Q4πεr)rˆ ur, which points in the radial direction. We enclose the charge by an imaginary sphere of radius r .We enclose the charge by an imaginary sphere of radius r called the “Gaussian surface.” Figure 4.2.2 A small area element on the surface of a sphere of radius r. In the above, we have chosen a sphere to be the Gaussian surface. However, it turns out that the shape of the closed surface can be arbitrarily chosen.We now study what happens when free charges are placed on a conductor. Generally, in the presence of a (generally external) electric field, the free charge in a conductor redistributes and very quickly reaches electrostatic equilibrium.
Non-Uniformly Charged Sphere. A non-conducting sphere of radius R has a non-uniform charge density that varies with the distance from its center as given by \[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\] where a is a constant. We require \(n \geq 0\) so that the charge density is not undefined at \(r = 0\).
• Surface S3 encloses no charges. Net flux through the surface is zero. The flux is negative at the upper part, and positive at the lower part, but these cancel. F = 0. • Surface S4 encloses both charges. Zero net charge enclosed, so equal flux enters and leaves, zero net .Apply the Gauss’s law strategy given above, where we work out the enclosed charge integrals separately for cases inside and outside the sphere. Solution Since the given charge density function has only a radial dependence and no dependence on direction, we have a spherically symmetrical situation.Child acquires electric charge by touching a charged metal sphere. Electrons coat each individual hair fiber and then repel each other. A charge distribution produces an electric field (E), and E exerts a force on a test charge (q 0). By moving q around a .Charging by conduction involves the contact of a charged object to a neutral object. Suppose that a positively charged aluminum plate is touched to a neutral metal sphere. The neutral metal sphere becomes charged as the result of being contacted by the charged aluminum plate.
The reasoning provided behind why the electric field inside a metallic conductive sphere is zero, in my textbook is - "In case of a metallic (conducting) sphere, the entire charge will reside on the outer surface of the sphere. Therefore .The lowest potential energy for a charge configuration inside a conductor is always the one where the charge is uniformly distributed over its surface. This is why we can assume that there are no charges inside a conducting sphere.
Consider a positive point charge Q located at the center of a sphere of radius r, as shown in Figure 4.2.1. The electric field due to the charge Q is 2 0 E=(/Q4πεr)rˆ ur, which points in the radial direction. We enclose the charge by an imaginary sphere of radius r .We enclose the charge by an imaginary sphere of radius r called the “Gaussian surface.” Figure 4.2.2 A small area element on the surface of a sphere of radius r. In the above, we have chosen a sphere to be the Gaussian surface. However, it turns out that the shape of the closed surface can be arbitrarily chosen.We now study what happens when free charges are placed on a conductor. Generally, in the presence of a (generally external) electric field, the free charge in a conductor redistributes and very quickly reaches electrostatic equilibrium.Non-Uniformly Charged Sphere. A non-conducting sphere of radius R has a non-uniform charge density that varies with the distance from its center as given by \[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\] where a is a constant. We require \(n \geq 0\) so that the charge density is not undefined at \(r = 0\).
• Surface S3 encloses no charges. Net flux through the surface is zero. The flux is negative at the upper part, and positive at the lower part, but these cancel. F = 0. • Surface S4 encloses both charges. Zero net charge enclosed, so equal flux enters and leaves, zero net .
Apply the Gauss’s law strategy given above, where we work out the enclosed charge integrals separately for cases inside and outside the sphere. Solution Since the given charge density function has only a radial dependence and no dependence on direction, we have a spherically symmetrical situation.Child acquires electric charge by touching a charged metal sphere. Electrons coat each individual hair fiber and then repel each other. A charge distribution produces an electric field (E), and E exerts a force on a test charge (q 0). By moving q around a .
non conducting solid sphere
The oldest surviving manual on western swordsmanship dates back to the 14th century, [1] although historical references date fencing schools back to the 12th century. [2] [3] [4] Modern fencing originated in the 18th century influenced by the Italian school of fencing of the Renaissance, and improved by the French school. [5] [6]
a no charge box surrounds a conducting metal sphere|0 charge in conductor