density distribution of particle in box Because of its mathematical simplicity, the particle in a box model is used to find approximate solutions for more complex physical systems in . See more Im considering buying a 110 volt mig welder, Ill mostly be working with sheet metal, some light tubing, and angle iron. Other than having an extra 10 amps what does the Hobart 135 have featurewise versus the 125? Which one would be the better choice?
0 · probability density of particle
1 · probability density in a box
2 · probability density distribution
3 · probability density 1d box
4 · particle in a box function
5 · particle in a box diagram
6 · particle in a box
7 · particle in 2 dimensional box
Weidmuller (Malaysia) Sdn Bhd No. 33, Jalan I-Park SAC4 Taman Perindustrian I-Park SAC 81400 Senai, Johor. Tel: +607 5959 652 Email: [email protected]
In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes the movement of a free particle in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between . See moreThe simplest form of the particle in a box model considers a one-dimensional system. Here, the particle may only move backwards and . See more
Because of its mathematical simplicity, the particle in a box model is used to find approximate solutions for more complex physical systems in . See more
junction box spider man ps4
• History of Quantum Mechanics• Finite potential well• Delta function potential• Gas in a box• Particle in a ring See more• Configuration integral (statistical mechanics), 2008. this wiki site is down; see this article in the web archive on 2012 April 28. See more(Hyper-)rectangular wallsIf a particle is trapped in a two-dimensional box, it may freely move in the $${\displaystyle x}$$ See moreThe probability density does not go to zero at the nodes if relativistic effects are taken to account via Dirac equation. See more
• Bransden, B. H.; Joachain, C. J. (2000). Quantum mechanics (2nd ed.). Essex: Pearson Education. ISBN 978-0-582-35691-7 See more
probability density of particle
This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density .To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution \[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \] for finding the particle around location \(x\) between the walls .
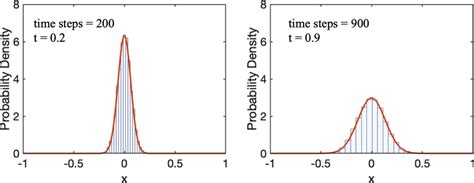
Figure \(\PageIndex{3}\): The probability density distribution \(|\psi_n(x)|^2\) for a quantum particle in a box for: (a) the ground state, \(n = 1\); (b) the first excited state, \(n = 2\); and, (c) the nineteenth excited state, \(n = .The probability density distribution for a quantum particle in a box for: (a) the ground state, ; (b) the first excited state, ; and, (c) the nineteenth excited state, . The probability density of finding a classical particle between x and depends .
A particle in a 1-dimensional box is a fundamental quantum mechanical approximation describing the translational motion of a single particle confined inside an infinitely deep well from which it cannot escape.
Particle in a Box Outline - Review: Schrödinger Equation - Particle in a 1-D Box. Eigenenergies. Eigenstates. Probability densities Figure \(\PageIndex{2}\): Visualizing the first six wavefunctions and associated probability densities for a particle in a two-dimensional square box (\(L_x=L_y=L\)). Use the slide bar to independently change either \(n_x\) or .
need to know the energy distribution of the allowed states. This is usually summarized by a function known as the density of states (DOS), which we represent by g(E). There will be .
particle. A classical particle of constant energy would have an equal probability of being found anywhere in the box since constant energy means constant speed. A quantum mechanical .In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes the movement of a free particle in a small space surrounded by impenetrable barriers.This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution |
To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution \[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \] for finding the particle around location \(x\) between the walls when the particle is in quantum state \(\psi_n\). Figure \(\PageIndex{3}\): The probability density distribution \(|\psi_n(x)|^2\) for a quantum particle in a box for: (a) the ground state, \(n = 1\); (b) the first excited state, \(n = 2\); and, (c) the nineteenth excited state, \(n = 20\).
junction box shallow
The probability density distribution for a quantum particle in a box for: (a) the ground state, ; (b) the first excited state, ; and, (c) the nineteenth excited state, . The probability density of finding a classical particle between x and depends on how much time the particle spends in this region. A particle in a 1-dimensional box is a fundamental quantum mechanical approximation describing the translational motion of a single particle confined inside an infinitely deep well from which it cannot escape.Particle in a Box Outline - Review: Schrödinger Equation - Particle in a 1-D Box. Eigenenergies. Eigenstates. Probability densities Figure \(\PageIndex{2}\): Visualizing the first six wavefunctions and associated probability densities for a particle in a two-dimensional square box (\(L_x=L_y=L\)). Use the slide bar to independently change either \(n_x\) or \(n_y\) quantum number and .
need to know the energy distribution of the allowed states. This is usually summarized by a function known as the density of states (DOS), which we represent by g(E). There will be much more about the DOS later in this section. It is defined .particle. A classical particle of constant energy would have an equal probability of being found anywhere in the box since constant energy means constant speed. A quantum mechanical particle of constant energy would have a maximum probability of being found in the center for n=1. But as n increases, the number of maxima & number of nodes .
probability density in a box
probability density distribution
In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes the movement of a free particle in a small space surrounded by impenetrable barriers.This principle states that for large quantum numbers, the laws of quantum physics must give identical results as the laws of classical physics. To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution |To illustrate how this principle works for a quantum particle in a box, we plot the probability density distribution \[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \] for finding the particle around location \(x\) between the walls when the particle is in quantum state \(\psi_n\). Figure \(\PageIndex{3}\): The probability density distribution \(|\psi_n(x)|^2\) for a quantum particle in a box for: (a) the ground state, \(n = 1\); (b) the first excited state, \(n = 2\); and, (c) the nineteenth excited state, \(n = 20\).
junction box supplier in ahmedabad
The probability density distribution for a quantum particle in a box for: (a) the ground state, ; (b) the first excited state, ; and, (c) the nineteenth excited state, . The probability density of finding a classical particle between x and depends on how much time the particle spends in this region. A particle in a 1-dimensional box is a fundamental quantum mechanical approximation describing the translational motion of a single particle confined inside an infinitely deep well from which it cannot escape.Particle in a Box Outline - Review: Schrödinger Equation - Particle in a 1-D Box. Eigenenergies. Eigenstates. Probability densities
Figure \(\PageIndex{2}\): Visualizing the first six wavefunctions and associated probability densities for a particle in a two-dimensional square box (\(L_x=L_y=L\)). Use the slide bar to independently change either \(n_x\) or \(n_y\) quantum number and .need to know the energy distribution of the allowed states. This is usually summarized by a function known as the density of states (DOS), which we represent by g(E). There will be much more about the DOS later in this section. It is defined .
probability density 1d box
The B618R is a round old work outlet box and is not listed for fixture support in the ceiling. Only approved ceiling boxes are allowed to support fixtures in the ceiling. These boxes will be permitted to support a minimum weight of 50 pounds. The B618R can be used in the ceiling as a junction box. Do not hang a
density distribution of particle in box|particle in a box diagram